1.1. 线性模型
以下是一组用于回归的方法,其中目标值被认为是输入变量的线性组合。用数学符号表示,假设 \hat{y} 是预测值,则有
\hat{y}(w, x) = w_0 + w_1 x_1 + … + w_p x_p
在整个模块中,我们把向量w=(w1,…,wp)记作 coef_ (系数),并把w0记作 intercept_ (截距).
要使用广义线性模型进行分类,请参阅 Logistic回归。
1.1.1. 普通最小二乘法
LinearRegression 用系数w=(w1,…,wp)拟合线性模型以使数据集的观察数据与预测值之间的差的平方和最小。其数学表达式为:
\min_{w} || X w – y||_2^2

LinearRegression的fit方法参数是数组X和y,该对象把线性模型的系数w 存储放在coef_成员变量中:
>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
>>> reg.coef_
array([0.5, 0.5])
普通最小二乘的系数估计取决于数据特征的独立性。如果特征是相关的,并且设计矩阵(design matrix) X 的各列近似线性相关的话, 那么,设计矩阵会趋向于奇异矩阵,导致最小二乘估计对观察数据中的随机误差变得高度敏感,这会产生很大的方差。 例如,在没有实验设计的情况下收集到的数据,这种多重共线性(multicollinearity)的情况可能真的会出现。
案例:
1.1.1.1. 普通最小二乘法的复杂度
该方法是使用X的奇异值分解来计算最小二乘的值。如果X是形状(n_samples, n_features)的矩阵,假设n_{samples}≥n_{features},则此方法的计算成本为 O(n_{samples}n_{features}^2) 。
1.1.2. 岭回归和分类
1.1.2.1. 岭回归(Ridge Regression)
岭(Ridge)回归通过对系数的大小进行惩罚来解决普通最小二乘的一些问题 。岭系数最小化的是带惩罚项的残差平方和:
\min_{w} || X w – y||_2^2 + \alpha ||w||_2^2
其中,α≥0是一个控制缩减量(amount of shrinkage)的复杂度参数: α的值越大, 缩减量就越大,线性模型的系数对共线性的鲁棒性越强。
与其他线性模型一样,岭(Ridge)的fit方法参数是数组X和y,该对象把线性模型的系数w 存储放在coef_成员变量中:
>>> from sklearn import linear_model
>>> reg = linear_model.Ridge(alpha=.5)
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5)
>>> reg.coef_
array([0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...
1.1.2.2. 岭分类(Ridge Classification)
该岭(Ridge)回归具有分类的变体 RidgeClassifier。该分类器首先将二进制目标值转换为{-1, 1},然后将问题视为回归任务,从而可以与上述相同优化目标。预测的类别跟回归器预测结果的正负有关。对于多类分类,该问题被视为多输出回归任务,预测的类列对应于具有最高值的输出。
使用最小二乘损失来拟合分类模型而不是更传统的逻辑损失( logistic losses)或合页损失(hinge losses)似乎是有问题的。但是实际上,所有这些模型都可以在准确率或精确度/召回率方面得出相似的交叉验证得分,而使用的惩罚最小二乘损失则RidgeClassifier允许对具有不同计算性能曲线的数值求解器(solvers )进行不同的选择。
在多类别任务上,RidgeClassifier可以训练地更快比起 LogisticRegression来说,因为它是只计算投影矩阵(X^TX)^{−1}X^T一次。
该分类器有时被称为带有线性核的最小二乘支持向量机(Least Squares Support Vector Machines)。
案例:
1.1.2.3. 岭回归的复杂度
此方法的复杂度与 普通最小二乘法相同。
1.1.2.4. 设置正则化参数:广义交叉验证
RidgeCV通过alpha参数的内置交叉验证来实现岭回归。该对象的工作方式与GridSearchCV相同,不同之处在于它默认使用通用交叉验证(GCV)方式,该方式是一种有效的留一法交叉验证(leave-one-out cross-validation):
>>> import numpy as np
>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13))
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
RidgeCV(alphas=array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06]))
>>> reg.alpha_
0.01
指定cv属性的值将触发使用GridSearchCV的交叉验证方式,例如cv=1010倍交叉验证,而不是通用交叉验证(GCV)。
参考资料
- “Notes on Regularized Least Squares”, Rifkin & Lippert (technical report, course slides).
1.1.3. Lasso
Lasso是一种估计稀疏系数的线性模型。由于它倾向于使用具有较少参数值,因此在某些情况下很有用,从而有效地减少解决方案所依赖的变量的数量。因此,Lasso 及其变体是压缩感知(compressed sensing)领域的基础。在某些条件下,它可以恢复非零权重的精确解(请参阅 压缩感知:使用L1先验(Lasso)进行的层析重建)。
在数学公式表达上,它由一个带有 ℓ_1 先验的正则项的线性模型组成。 其最小化的目标函数是:
\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w – y||_2 ^ 2 + \alpha ||w||_1}
lasso估计解决了加上惩罚项α||w||_1的最小二乘的最小化,其中, α 是一个常数,||w||_1 是参数向量的 ℓ_1-norm 范数。
Lasso实现使用了 coordinate descent (坐标下降算法)来拟合系数。 另一种实现方法在最小角度回归(Least Angle Regression )中:
>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha=0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1)
>>> reg.predict([[1, 1]])
array([0.8])
该函数lasso_path对较低级别的任务很有用,因为它够通过搜索所有可能的路径上的值来计算系数。
案例:
注意:使用 Lasso 进行特征选择
由于 Lasso regression 能够产生稀疏模型,所以它可以用来特征选择,详情可以参见 基于L1的特征选择。
以下两个参考文献解释了scikit-learn的坐标下降求解器(coordinate descent solver)的迭代过程,以及用于收敛控制的对偶间隙(duality gap)计算。
参考文献
- “Regularization Path For Generalized linear Models by Coordinate Descent”, Friedman, Hastie & Tibshirani, J Stat Softw, 2010 (Paper).
-
“An Interior-Point Method for Large-Scale L1-Regularized Least Squares,” S. J. Kim, K. Koh, M. Lustig, S. Boyd and D. Gorinevsky, in IEEE Journal of Selected Topics in Signal Processing, 2007 (Paper)
1.1.3.1. 设置正则化参数
alpha参数控制模型系数的稀疏程度。
1.1.3.1.1. 使用交叉验证
scikit-learn提供能通过交叉验证来设置Lasso 的alpha参数的对象有:LassoCV和LassoLarsCV。 LassoLarsCV是基于下面解释的最小角回归算法。
对于具有许多共线特征的高维数据集, LassoCV通常是首选。但是,LassoLarsCV具有能够探索到更多alpha参数值的优势,并且如果样本数量与特征数量相比非常少的话,LassoLarsCV则通常比LassoCV快。
1.1.3.1.2. 基于信息标准的模型选择
作为替代方案,估计器(estimator) LassoLarsIC建议使用Akaike信息准则(AIC)和Ba支持信息准则(BIC)。使用基于信息准则的方法寻找 alpha 的最优值是一种计算成本较低的方法,因为这种方法中正则化路径只计算一次而不是使用k-fold交叉验证时的k+1次。 然而,这类准则需要对解的自由度进行适当的估计,是为大样本(渐近结果)导出的,并假定模型是正确的(即数据实际上是由该模型生成的)。 当问题条件数不好(特征多于样本)时,它们可能会崩溃。
案例:
1.1.3.1.3. 与SVM的正则化参数比较
alpha 和 SVM 的正则化参数 C 之间的等式关系是 alpha = 1 / C 或者 alpha = 1 / (n_samples * C) , 并依赖于估计器(estimator)和模型优化的确切的目标函数。
1.1.4. 多任务 Lasso(Multi-task Lasso)
MultiTaskLasso是一个联合估计多元回归问题的稀疏系数的线性模型:y是一个(n_samples, n_tasks)形状的2D矩阵。其约束条件是所有回归问题(也称为任务)所选的特征都是相同。
下图比较了通过使用简单的 Lasso 或 MultiTaskLasso 得到的矩阵W 中非零的位置。 Lasso 估计产生分散的非零值,而 MultiTaskLasso 的一整列都是非零的。
拟合时间序列模型,强制让任何激活特征在任何时候都是激活的。
案例:
从数学上讲,它包含一个经过混合训练的线性模型ℓ_1 ℓ_2-规范化。最小化的目标函数是:
\min_{w} { \frac{1}{2n_{\text{samples}}} ||X W – Y||_{\text{Fro}} ^ 2 + \alpha ||W||_{21}}
其中\text{Fro} 表示Frobenius规范
||A||_{\text{Fro}} = \sqrt{\sum_{ij} a_{ij}^2}
其中 \ell_1 \ell_2
||A||_{2 1} = \sum_i \sqrt{\sum_j a_{ij}^2}.
MultiTaskLasso类也使用了坐标下降法(coordinate descent)来拟合系数。
1.1.5. 弹性网(Elastic Net)
ElasticNet 是一种使用\ell_1和\ell_2先验作为正则项训练的线性回归模型。这种组合允许学习稀疏模型,其中几乎没有权重是非零的Lasso,同时仍保持的正则化属性Ridge。我们控制凸组合\ell_1和\ell_2使用l1_ratio 参数。
弹性网(Elastic Net)在很多特征相互关联的情况下是非常有用的。Lasso 很可能只随机考虑这些特征中的一个,而弹性网(Elastic Net)更倾向于选择两个。
在实践中,Lasso 和 Ridge 之间权衡的一个优势是它允许弹性网(Elastic-Net)在循环过程中继承 岭(Ridge) 的稳定性。
最小化的目标函数:
\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w – y||_2 ^ 2 + \alpha \rho ||w||_1 + \frac{\alpha(1-\rho)}{2} ||w||_2 ^ 2}

该ElasticNetCV类可以通过交叉验证来设置 alpha (α) 和 l1_ratio (ρ) 参数的值。
案例:
以下两个参考文献解释了scikit-learn的坐标下降求解器(coordinate descent solver)中的迭代过程,以及用于收敛控制的对偶间隙(duality gap)计算。
参考文献
- “Regularization Path For Generalized linear Models by Coordinate Descent”, Friedman, Hastie & Tibshirani, J Stat Softw, 2010 (Paper).
-
“An Interior-Point Method for Large-Scale L1-Regularized Least Squares,” S. J. Kim, K. Koh, M. Lustig, S. Boyd and D. Gorinevsky, in IEEE Journal of Selected Topics in Signal Processing, 2007 (Paper)
1.1.6. 多任务弹性网(Multi-task Elastic-Net)
MultiTaskElasticNet是一个对多变量回归问题估计其稀疏系数的弹性网(Elastic-Net)模型:Y是一个形状为(n_samples, n_tasks)的2D矩阵。其约束条件是所有回归问题(也称为任务)所选的特征都是相同。
从数学上讲,它是一个混合了ℓ_1 ℓ_2 先验 和 ℓ_2 先验作为正则化项的线性模型。 目标函数的最小化如下所示:
\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W – Y||_{\text{Fro}}^2 + \alpha \rho ||W||_{2 1} + \frac{\alpha(1-\rho)}{2} ||W||_{\text{Fro}}^2}
MultiTaskElasticNet使用坐标下降(coordinate descent)算法来拟合系数。
MultiTaskElasticNetCV可以通过交叉验证来设置 alpha (α) 和 l1_ratio (ρ) 参数的值。
1.1.7. 最小角回归(Least Angle Regression)
最小角回归(LARS)是由Bradley Efron,Trevor Hastie,Iain Johnstone和Robert Tibshirani开发的用于高维数据的回归算法。LARS与前向逐步回归(forward stepwise regression)相似。在每个步中,它都会找到与预测结果最相关的特征。当存在多个相等的相关特征时,它没有继续利用相同的特征, 而是在这些特征中找出等角的方向。
LARS的优点:
- 在特征数量明显大于样本数量的情况下,它在数值上是有效的。
- 它的计算速度与前向选择一样快,并且复杂度与普通最小二乘法相同。
- 它会产生一个完整的分段线性求解路径,这在交叉验证或类似的模型调整尝试中很有用。
- 如果两个特征与预测结果几乎具有相等相关关系的话,则它们的系数应有大致相同的增长速率。因此,该算法的表现与我们的直觉所期望的一样,并且更加稳定。
- 可以轻松对其进行修改,可以为其他估计器(例如Lasso)提供解。
LARS 的缺点:
- 因为LARS是基于残差的迭代拟合,所以它似乎对噪声的影响特别敏感。Weisberg的Efron et al. (2004) Annals of Statistics论文的讨论部分中详细地讨论了此问题。
可以通过估计器(estimator) Lars或其底层实现lars_path或lars_path_gram 来使用LARS模型。
1.1.8. LARS Lasso
LassoLars 是使用LARS算法实现的Lasso模型,与基于坐标下降(coordinate descent)算法不同, 它可以得到一个精确解。这个解作为其系数的范数是分段线性函数。
>>> from sklearn import linear_model
>>> reg = linear_model.LassoLars(alpha=.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
LassoLars(alpha=0.1)
>>> reg.coef_
array([0.717157..., 0. ])
案例:
Lars算法提供了一个几乎无代价的沿着正则化参数的系数的完整路径,因此常见的操作是使用函数lars_path 或lars_path_gram来检索路径。
1.1.8.1. 数学公式
该算法和前向逐步回归(forward stepwise regression)类似,但是它没有在每一步包含变量, 它估计的参数是根据与其他剩余变量的相关性来增加的。
在 LARS 的解中,没有给出一个向量的结果,而是由一条曲线表示,显示参数向量的L_1范式的每个值的解。 完全的参数路径存在 coef_path_ 成员变量中。它的 size 是 (n_features, max_features+1),第一列始终为零。
参考文献:
- Hastie et al.的最小角回归中论文论文中详细介绍了原始算法。
1.1.9. 正交匹配追踪(OMP)
OrthogonalMatchingPursuit和orthogonal_mp实现OMP算法,用非零系数(即ℓ_0 伪范数(pseudo-norm))来近似线性模型的拟合。
作为最小角度回归等前向特征选择方法的一种,正交匹配追踪可以使用固定数量的非零元素来逼近最优解向量:
\underset{\gamma}{\operatorname{arg\,min\,}} ||y – X\gamma||_2^2 \text{ subject to } ||\gamma||_0 \leq n_{\text{nonzero_coefs}}
正交匹配追踪也可以针对特定误差而不是特定数量的非零系数。这可以表示为:
\underset{\gamma}{\operatorname{arg\,min\,}} ||\gamma||_0 \text{ subject to } ||y-X\gamma||_2^2 \leq \text{tol}
OMP基于贪婪算法,该算法在每个步骤中都包括与当前残差最相关的原子(atom)。它与更简单的匹配追踪(MP)方法相似,但比它更优的是,OMP在每次迭代中,使用在先前选择的字典元素的空间上的正交投影来重新计算残差。
案例:
参考资料:
- https://www.cs.technion.ac.il/~ronrubin/Publications/KSVD-OMP-v2.pdf
-
用时频词典进行匹配,SG Mallat,Z。Zhang,
1.1.10. 贝叶斯回归(Bayesian Regression)
贝叶斯回归技术可用于在估计过程中包含正则化参数: 正则化参数的选择不是通过人为进行设置的,而是根据手头上的数据来调整的。
这可以通过在模型的超参数上引入无信息先验(uninformative priors)来完成。Ridge回归和分类中使用的ℓ_2正则化相当于在高斯先验概率下为系数w找到精确度为λ^{−1}的最大后验估计值。该方法并不需要人工设置lambda,而是将其视为要从数据中估计的随机变量。
为了得到一个全概率模型,输出y 可以认为是关于 X_w 的高斯分布:
p(y|X,w,\alpha) = \mathcal{N}(y|X w,\alpha)
在这里\alpha也是作为一个变量,需要通过数据估计得到。
贝叶斯回归的优点:
- 它能根据手头的数据进行改变。
- 它能在估计过程中引入正则项的参数。
贝叶斯回归的缺点:
- 模型的推断可能很耗时。
参考资料
- A good introduction to Bayesian methods is given in C. Bishop: Pattern Recognition and Machine learning
- Original Algorithm is detailed in the book
Bayesian learning for neural networksby Radford M. Neal
- Original Algorithm is detailed in the book
1.1.10.1. 贝叶斯岭回归(Bayesian Ridge Regression)
BayesianRidge 是一个求解回归问题的概率模型。 其中模型的参数w的先验值通过球面高斯(spherical Gaussian)给出:
p(w|\lambda) = \mathcal{N}(w|0,\lambda^{-1}\mathbf{I}_{p})
α 和 λ 的先验分布选择为伽马分布,该分布与高斯分布成共轭先验关系。这样产生的模型称为*贝叶斯岭回归(Bayesian Ridge Regression)*,与经典模型岭回归(Ridge)相似。
参数 w, α 和 λ 是在模型拟合的时候一起被估算出来的。 正则化的超参数α 和 λ 通过最大化对数边际概率(log marginal likelihood)来估算的 。 scikit-learn实现基于(Tipping,2001)附录A中描述的算法,其中参数α 和 λ的更新算法来自(MacKay,1992)的建议。可以修改超参数alpha_init和lambda_init的值来设置最大化过程的初始值。
还有四个超参数, 伽玛先验分布的α_1, α_2, λ_1 和 λ_2 , α 和 λ。这些通常被选择为*非信息性的(non-informative)*。默认情况下α_1=α_2=λ_1=λ_2=10^{−6}。
贝叶斯岭回归(Bayesian Ridge Regression)用于回归问题:
>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge()
当模型拟合好以后, 就可以用来预测新的观测值:
>>> reg.predict([[1, 0.]])
array([0.50000013])
可以这样获得模型的权重参数w
>>> reg.coef_
array([0.49999993, 0.49999993])
由于贝叶斯框架与普通最小二乘的权重略有不同。但是,贝叶斯岭回归对于病态问题(ill-posed)更加健壮。
案例:
参考文献:
- Section 3.3 in Christopher M. Bishop: Pattern Recognition and Machine Learning, 2006
- David J. C. MacKay, Bayesian Interpolation, 1992.
- Michael E. Tipping, Sparse Bayesian Learning and the Relevance Vector Machine, 2001.
1.1.10.2. 自动关联确定(Automatic Relevance Determination)-ARD
ARDRegression与贝叶斯岭回归(Bayesian Ridge Regression)非常相似,但可以学习到更稀疏的模型权重参数w[1] [2]。
ARDRegression放弃球形高斯分布的假设(assumption of the Gaussian being spherical) 在w上添加了一个不同的先验分布。
与贝叶斯岭回归(Bayesian Ridge Regression)不同的是, w上的分布被假定为是一个与坐标轴平行的椭圆形高斯分布。
这意味着每一个权重系统w_i 是从高斯分布抽取的,此高斯分布以0位中心并且有一个精度λ_i:
p(w|\lambda) = \mathcal{N}(w|0,A^{-1})
其中 \text{diag}(A) = \lambda = {\lambda_{1},…,\lambda_{p}}。
与贝叶斯岭回归(Bayesian Ridge Regression)相反,每个w_i有自己的标准差λ_i。在所有λ_i上的先验分布被选择为由超参数λ_1和λ_2给出的相同的伽马分布(gamma distribution) 。
ARD在文献中也称为稀疏贝叶斯学习(Sparse Bayesian Learning)和 关联矢量机(Relevance Vector Machine) [3] [4]。
案例:
参考资料:
[1]Christopher M. Bishop: Pattern Recognition and Machine Learning, Chapter 7.2.1
[2] David Wipf and Srikantan Nagarajan: A new view of automatic relevance determination
[3] Michael E. Tipping: Sparse Bayesian Learning and the Relevance Vector Machine
[4] Tristan Fletcher: Relevance Vector Machines explainedhttp://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.651.8603&rep=rep1&type=pdf)
1.1.11. 逻辑回归(Logistic regression)
虽然有逻辑回归这个名称,但它是用于分类而不是回归的线性模型。逻辑回归(Logistic regression)在文献中也称为logit回归,最大熵分类(maximum-entropy classification (MaxEnt)),或 对数线性分类器(log-linear classifier)。在此模型中,使用logistic函数把单次试验(single trial)的可能的输出结果建模为概率分布。
LogisticRegression实现了包括二分类(binary)、 一对多分类(one-vs-rest)及多项式逻辑回归,并带有可选的L_1 和L_2 正则化的逻辑回归。
注意:
默认情况下,虽然在机器学习中应用正则化很常见,但在统计学中却不常见。正则化的另一个优点是可以提高数值稳定性。没有正则化等于将参数C设置为很高的值。
作为优化问题,带L_2惩罚项的二分类逻辑回归要最小化下面的代价函数(cost function):
\min_{w, c} \frac{1}{2}w^T w + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1) .
类似的, 带有L_1正则化的逻辑回归优化下面的问题:
\min_{w, c} \frac{1 – \rho}{2}w^T w + \rho |w|_1 + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1),
弹性网(Elastic Net)正则项是ℓ_1 和 ℓ_2的组合,它优化下面的代价函数(cost function):
\min_{w, c} \frac{1 – \rho}{2}w^T w + \rho |w|_1 + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1),
其中\rho控制ℓ_1和 ℓ_2正则项的惩罚力度(它对应于l1_ratio参数)。
注意, 在这个记法中, 假定了第i次试验的观测值 y_i 在集合 −1,1 中取值。我们还可以看到,当\rho = 1的时候弹性网(Elastic-Net)等效于ℓ_1, 当\rho = 0的时候弹性网((Elastic-Net)等效于ℓ_2。
类LogisticRegression 中实现的求解器(solvers)为“ liblinear”,“ newton-cg”,“ lbfgs”,“ sag”和“ saga”:
求解器(solvers)“ liblinear”使用坐标下降(CD)算法,并依赖于scikit-learn附带的优秀的C ++库 LIBLINEAR。但是,liblinear库实现的CD算法无法学习到真正的多项式(多类)模型。作为替代方案,优化问题是以”one-vs-rest”的方式分解的, 因此对所有类都分别进行了binary classifier的训练。这都发生在底层,因此使用此求解器(solvers)的 LogisticRegression的实例类型像一个多类分类器。对于ℓ_1正则化,sklearn.svm.l1_min_c允许计算C的下限,以便获得一个非空的模型(non “null” model)。
“ lbfgs”,“ sag”和“ newton-cg”求解器(solvers)仅支持ℓ_2 正则化或不支持正则化,并且发现对于某些高维数据来说模型收敛更快。把 multi_class 设置成 “multinomial” 可以学习到一个真正的多项式逻辑回归模型[5],这意味着与默认的 “one-vs-rest” 相比, 它的概率分布估计应该被更好地进行校准。
“sag”求解器(solvers)使用随机平均梯度下降(Stochastic Average Gradient descent)[6]算法。当样本数量和特征数量都很大时,它在大型数据集上比其他求解器运行更快。
“ saga”求解器(solvers)[7]是“ sag”的一种变体,它也支持penalty="l1"。因此,这是求解稀疏多项式逻辑回归的首选求解器(solvers)。它也是唯一支持 penalty="elasticnet"的求解器(solvers)。
“ lbfgs”是一种优化算法,与Broyden–Fletcher–Goldfarb–Shanno算法[8]类似。建议将“ lbfgs”求解器(solvers)用于较小的数据集,但如果用于较大的数据集,其性能会受到影响。[9]
下表总结了每个求解器(solvers)支持的惩罚项:
| 求解器(solvers) | |||||
|---|---|---|---|---|---|
| 惩罚项 | “liblinear” | “lbfgs” | “newton-cg” | “sag” | “saga” |
| 多项式+ L2 惩罚项 | 不支持 | 支持 | 支持 | 支持 | 支持 |
| OVR + L2 惩罚项 | 支持 | 支持 | 支持 | 支持 | 支持 |
| Multinomial + L1 惩罚项 | 不支持 | 不支持 | 不支持 | 不支持 | 支持 |
| OVR + L1 惩罚项 | 支持 | 不支持 | 不支持 | 不支持 | 支持 |
| 弹性网(Elastic-Net) | 不支持 | 不支持 | 不支持 | 不支持 | 支持 |
| 没有惩罚项 | 不支持 | 支持 | 支持 | 支持 | 支持 |
| 行为(Behaviors) | |||||
| 处罚拦截(Penalize the intercept) (bad) | 支持 | 不支持 | 不支持 | 不支持 | 不支持 |
| 在大型数据集上运行更快 | 不支持 | 不支持 | 不支持 | 支持 | 支持 |
| 在没有放缩的数据集上更健壮 | 支持 | 支持 | 支持 | 不支持 | 不支持 |
默认情况下使用“ lbfgs”求解器(solver),由于它的健壮性。对于大型数据集来说,“saga”求解器(solver)通常更快。对于大型数据集,您还可以考虑使用SGDClassifier 和“对数(log)”损失,该损失可能运行更快,但需要更多调整。
案例:
与liblinear的区别:
当 fit_intercept=False 和 拟合得到的 coef_ 是0 (或) 用于预测的数据是 0 的时候,使用参数为solver=liblinear的LogisticRegression类或 LinearSVC 类 与 直接使用外部库liblinear 所获得的分数可能会有一些差别。 这是因为对于那些 decision_function 为zero的样本,LogisticRegression 和 LinearSVC 给出的预测是负类,而liblinear库给出的预测 是正类。请注意 一个参数为 fit_intercept=False 并且在很多样本上 decision_function 为0的模型很可能是一个欠拟合的坏模型,并且建议您设置 fit_intercept=True 并且增加 intercept_scaling的值。
注意:稀疏逻辑回归的特征选择
带ℓ_1惩罚的逻辑回归会产生稀疏模型(sparse model),因此可用于特征选择,详情请参见基于L1的特征选择。
注意:P值估计
在不带惩罚项的情况下,有可能获得系数的p值和置信区间。“statsmodels package https://pypi.org/project/statsmodels/`支持这一方法。在sklearn中,也可以使用bootstrapping来达到这一目的。
LogisticRegressionCV通过内置的交叉验证实现逻辑回归,它根据scoring属性来查找参数C和l1_ratio的最佳值。由于热启动(warm-starting),发现“newton-cg”,“ sag”,“ saga”和“ lbfgs”求解器(solvers)对于高维密集数据运行更快(请参阅词汇表)。
参考资料:
[5] Christopher M. Bishop: Pattern Recognition and Machine Learning, Chapter 4.3.4
[6] Mark Schmidt, Nicolas Le Roux, and Francis Bach: Minimizing Finite Sums with the Stochastic Average Gradient.
[7] Aaron Defazio, Francis Bach, Simon Lacoste-Julien: SAGA: A Fast Incremental Gradient Method With Support for Non-Strongly Convex Composite Objectives.
[8] https://en.wikipedia.org/wiki/Broyden%E2%80%93Fletcher%E2%80%93Goldfarb%E2%80%93Shanno_algorithm
[9] “Performance Evaluation of Lbfgs vs other solvers”
1.1.12. 随机梯度下降(Stochastic Gradient Descent) – SGD
机梯度下降(Stochastic gradient descent)是拟合线性模型的一个简单而高效的方法。在样本数量(和特征数量)很大时,该方法非常有用。 方法 partial_fit 可用于 online learning (在线学习)或基于 out-of-core learning (外存的学习)。
SGDClassifier和SGDRegressor分别用于拟合分类问题和回归问题的线性模型,可以使用不同的(凸)损失函数和不同的惩罚。例如,当设置loss="log"时,SGDClassifier 拟合出一个逻辑回归模型,而当设置loss="hinge"时,它会拟合出线性支持向量机(SVM)。
参考资料
1.1.13. 感知机(Perceptron)
感知机(Perceptron)是适合大规模学习另一种简单分类算法。默认情况下:
- 它不需要学习率。
- 它不需要正则化处理。
- 仅使用错误样本更新模型。
最后一点表明使用合页损失(hinge loss)的感知机(Perceptron)比使用合页损失(hinge losses)的随机梯度下降(SGD)略快,所得模型更稀疏。
1.1.14. 被动攻击算法(Passive Aggressive Algorithms)
被动攻击算法(The passive-aggressive algorithms)是一个用于大规模学习的算法家族。 他们与感知机(Perceptron)相似,因为他们不需要学习率。 然而, 与感知器不同的是,他们包括了一个正则化参数 C。
对于分类问题,PassiveAggressiveClassifier可以与 loss='hinge'(PA-I)或loss='squared_hinge'(PA-II)一起使用。对于回归问题, PassiveAggressiveRegressor可以与 loss='epsilon_insensitive'(PA-I)或 loss='squared_epsilon_insensitive'(PA-II)一起使用。
参考文献:
- “Online Passive-Aggressive Algorithms” K. Crammer, O. Dekel, J. Keshat, S. Shalev-Shwartz, Y. Singer – JMLR 7 (2006)
1.1.15. 鲁棒回归(Robust regression):处理异常点(outliers)和模型错误
鲁棒回归(Robust regression) 适用于回归模型包含损坏数据(如异常点或模型错误)的情况。
1.1.15.1. 各种使用场景与相关概念
处理包含异常点的损坏数据时,需要记住以下几点:
- 异常点在 X 中还是在 y 中?
| 在y中的异常点 | 在X中的异常点 |
|---|---|
 |
 |
- 异常点的数量与误差幅度的关系
虽然说外围点(outlying points)的数量很重要,但是其中有多少是异常点也很重要。(The number of outlying points matters, but also how much they are outliers.)。
| 数量少的异常点 | 数量大的异常点 |
|---|---|
 |
 |
鲁棒回归(Robust regression)的一个非常重要的概念就是击穿点(breakdown point)。该点是指那些用于拟合开始丢失内在数据的超出拟合范围的数据。
注意,一般来说,在高维(比较大的 n_features )情况中,鲁棒的拟合是非常困难的.这里的鲁棒模型可能无法在这些设置中工作。
权衡: 该用哪个估计器 ?
Scikit-learn提供了3种强大的鲁棒回归估计器: RANSAC, Theil Sen和 HuberRegressor。
- HuberRegressor应该比 RANSAC和 Theil Sen更快,除非样本数量非常大,即
n_samples>>n_features。这是因为 RANSAC和 Theil Sen 适合的较小的数据集。但是, Theil Sen 和 RANSAC的默认参数都不太可能像 HuberRegressor一样强大 。
如果您不知道用什么估计器的时候,就使用RANSAC吧。
1.1.15.2. RANSAC:随机抽样一致性算法
RANSAC (RANdom SAmple Consensus) 在完整数据集的所有正常点(inliers)的随机子集上拟合一个模型。
RANSAC是一种不确定性算法,仅以一定概率生成一个合理结果,该结果取决于迭代次数(请参阅 max_trials参数)。它通常用于线性和非线性回归问题,在摄影测量计算机视觉领域特别受欢迎。
该算法将完整的输入样本数据划分为可能会受到噪声干扰的正常点(inliers)和一些异常点(outliers),这些异常点的可能是由有关数据的错误测量或无效假设引起的。所以,RANSAC产生的模型是只在确定的正常点(inliers)样本数据上估计出来的。
1.1.15.2.1. 算法细节
每次迭代要执行以下步骤:
- 从原始数据中随机选择
min_samples个样本,然后检查这些样本是否是有效的(请看is_data_valid)。 - 在上一步选出的随机子集上拟合一个模型 (
base_estimator.fit) 并检查估计出的模型是否有效 (请看is_model_valid)。 - 通过计算样本与估计出的模型的预测值之间的残差(residuals)把所有样本数据分为正常点(inliers) 或 异常点(outliers)样本集合 (
base_estimator.predict(X) - y) 。 那些绝对残差小于残差阈值residual_threshold的所有样本被认为是 正常点(inliers)。 - 如果正常点(inliers)样本的数量达到最大值就把拟合好的模型保存下来作为最优模型。 如果 当前估计出的模型与历史最优模型有同样多的正常点(inlier)样本量的话, 那么只有在当前估计出的模型的得分更高的时候它才会被认为是最优模型。
上述几个步骤会一直执行,直到迭代次数达到最大迭代次数(max_trials) 或 满足了其中一个特定的停止条件 (请看 stop_n_inliers 和 stop_score)。 最终的模型是使用所有正常点(inliers)样本(一致集(consensus set))估计得到的。 而最后使用的所有正常点(inliers)样本是由之前迭代过程中确定的历史最优模型在原始样本集上挑选出的。
is_data_valid 和 is_model_valid 函数k可以辨识和拒绝随机子样本集的退化组合( degenerate combinations)。 如果不需要使用估计的模型来识别退化情况,那么 is_data_valid 应该被使用,因为它在拟合模型之前即已被调用 ,从而获得更好的计算性能。
案例:
参考资料:
- https://en.wikipedia.org/wiki/RANSAC
-
“Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography” Martin A. Fischler and Robert C. Bolles – SRI International (1981)
-
“Performance Evaluation of RANSAC Family” Sunglok Choi, Taemin Kim and Wonpil Yu – BMVC (2009)
1.1.15.3. Theil-Sen 估计器: 广义中值估计器
TheilSenRegressor估计器在多维度数据中使用广义中值。因此,它对于多元异常点是鲁棒的。但是请注意,估计器的鲁棒性随问题的维度增加而迅速降低。在高维情形中它会丧失鲁棒性并且会比普通最小二乘法更差。
案例:
参考资料:
1.1.15.3.1. 理论方面的思考
TheilSenRegressor就渐近效率和无偏估计而言,它可与普通最小二乘(OLS)相提并论。与OLS相比,Theil-Sen是一种非参数方法,这意味着它不对数据的基础分布进行任何假设。由于Theil-Sen是基于中位数的估计器,因此对于损坏的数据(也称为异常点)而言,它更加鲁棒。在单变量设置下,如果进行简单的线性回归,Theil-Sen的击穿点(breakdown point)约为29.3%,这意味着它可以忍受高达29.3%的损坏数据。
在scikit-learn中TheilSenRegressor的实现遵循使用空间中位数的多元线性回归模型[10]的推广,而空间中位数是到多维数据的中位数[11]的推广。
就时间与空间复杂度来说, Theil-Sen 可以依据下式进行伸缩(scale):
\binom{n_{\text{samples}}}{n_{\text{subsamples}}}
这使得在具有大量样本和大量特征的问题上进行全面的应用是不可行的。 因此, 通过只考虑所有可能组合的一个随机子集,可以选择子种群的大小来限制时间和空间复杂性。
案例:
References:
参考文献:
[10] Xin Dang, Hanxiang Peng, Xueqin Wang and Heping Zhang: Theil-Sen Estimators in a Multiple Linear Regression Model.
[11] 20.Kärkkäinen and S. Äyrämö: On Computation of Spatial Median for Robust Data Mining.
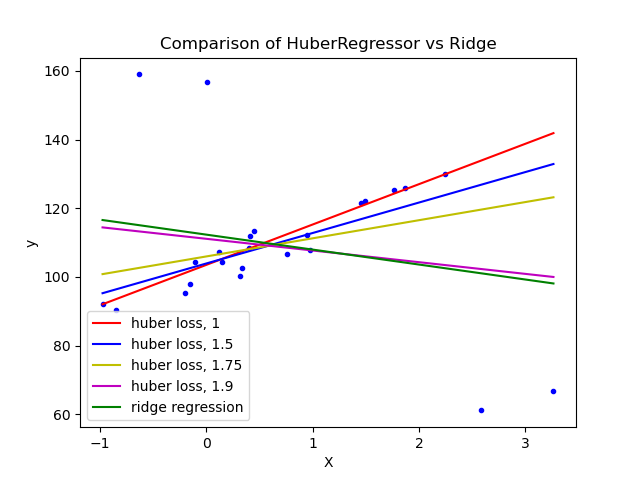
1.1.15.4. Huber 回归
HuberRegressor与Ridge有所不同,因为它将一个线性损失应用到那些被判断为是异常点(outliers)的样本上。如果该样本的绝对误差小于某个阈值,则将其分类为正常点(inlier)。这与TheilSenRegressor 和RANSACRegressor是有区别的,因为它不会忽略异常点(outliers)的影响而是会给异常点(outliers)设置一个较小的权重。
HuberRegressor要最小化的损失函数是:
\min_{w, \sigma} {\sum_{i=1}^n\left(\sigma + H_{\epsilon}\left(\frac{X_{i}w – y_{i}}{\sigma}\right)\sigma\right) + \alpha {||w||_2}^2}
其中
H_{\epsilon}(z) = \left{\begin{matrix} z^2,& \text {if } |z| < \epsilon, \\2\epsilon|z| - \epsilon^2, & \text{otherwise} \end{matrix}\right.
建议将epsilon参数设置为1.35,以达到95%的统计效率。
1.1.15.5. 注意事项
HuberRegressor与把损失参数设为 huber的SGDRegressor的区别在以下几个方面。
HuberRegressor是尺度不变的(scaling invariant)。一旦设置了epsilon,把X和y放大或缩小不同的值将会产生对异常点(outliers)一样的鲁棒性,就跟没有缩放之前一样。但是在SGDRegressor中,如果调整了X和y的尺度的话,epsilon也得被重新设置。HuberRegressor在样本数较少的数据上使用时应该更有效率,而SGDRegressor在训练数据上需要多次迭代才能产生相同的鲁棒性。
案例:
参考文献:
- Peter J. Huber, Elvezio M. Ronchetti: Robust Statistics, Concomitant scale estimates, pg 172
请注意,此估计器与鲁邦回归(http://www.ats.ucla.edu/stat/r/dae/rreg.htm)的R语言实现不同,因为R语言实现了加权最小二乘,该方法是基于残差比给定阈值大多少而产生的权重被赋予了每个样本。
1.1.16. 项式回归:用基函数展开线性模型
机器学习中的一种常见模式是使用在数据的非线性函数上训练的线性模型。这种方法保持了线性方法的一般快速性能,同时允许它们适应更大范围的数据。
例如,可以通过系数构造多项式特征(polynomial features)来扩展简单的线性回归 。在标准线性回归的情况下,对于二维数据,一个用于拟合二维数据的模型如下所示:
\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2
如果我们想要用抛物面拟合数据而不是平面,我们可以用二阶多项式组合特征,使模型看起来像这样:
\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_1 x_2 + w_4 x_1^2 + w_5 x_2^2
上面的模型看起来仍然是一个线性模型(尽管有些令人吃惊),为了说明这一点,我们尝试创建一个新的变量:
z = [x_1, x_2, x_1 x_2, x_1^2, x_2^2]
用上面的变量重新变换数据,原来的问题就可以写成这样:
\hat{y}(w, z) = w_0 + w_1 z_1 + w_2 z_2 + w_3 z_3 + w_4 z_4 + w_5 z_5
我们看到,所得多项式回归与我们所见过的线性模型是一样的(即模型在w参数上是线性组合),并且可以用线性模型的求解方法来解决。考虑到可以对由这些基本函数构建的高维空间进行线性拟合, 该模型在拟合更大范围的数据时确实有非常大的弹性和灵活性。
这里有个例子,它将上述想法用于一维数据, 使用了不同阶的多项式特征:
该图是使用PolynomialFeatures转换器所创建的,该转换器将输入的数据矩阵转换为给定阶数的新数据矩阵。其用法如下:
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
[2, 3],
[4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])
X 的各个特征分量已经由[x_1, x_2] 转换为[1, x_1, x_2, x_1^2, x_1 x_2, x_2^2],并且可被用于任意的线性模型。
这种类型的预处理器可以用管道(Pipeline)集成为一个工作流。 这样就可以用单个对象表示一个简单的多项式回归器,如下所示:
>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
('linear', LinearRegression(fit_intercept=False))])
>>> # 拟合一个阶数为3的多项式数据
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2., 1., -1.])
在多项式特征上训练好的线性模型可以准确的恢复输入多项式系数。
在某些情况下,没有必要包括任意单个特征的更高阶特征,而只需包含所谓的交互特征(interaction features)。这些可以通过把PolynomialFeatures中的参数设置成 interaction_only=True来得到。
比如说, 当处理布尔特征的时候, 对所有的n,有x_i^n = x_i,这时候高阶多项式基是没用的; 但是任意两个布尔特征的乘积x_ix_j 却表达了两个布尔特征的联合(conjunction)。这样,我们就可以用线性分类器来求解异或(XOR)问题。
>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
[1, 0, 1, 0],
[1, 1, 0, 0],
[1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, max_iter=10, tol=None,
... shuffle=False).fit(X, y)
最后,这个线性分类器的预测相当完美:
>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0
©2007-2019,scikit-learn开发人员(BSD许可证)。 显示此页面源码

 PythonOK
PythonOK












 2.7. 新奇点与离群点检测(Novelty and Outlier Detection)
2.7. 新奇点与离群点检测(Novelty and Outlier Detection) 2.1. 高斯混合模型(Gaussian mixture models)
2.1. 高斯混合模型(Gaussian mixture models) 2.4. 双聚类(Biclustering)
2.4. 双聚类(Biclustering) 2.2. 流形学习(Manifold learning)
2.2. 流形学习(Manifold learning)