2.9. 神经网络模型（无监督）

2.9.1. 受限玻尔兹曼机器(Restricted Boltzmann machines)

受限玻尔兹曼机（RBM）是基于概率模型的无监督非线性特征学习器。将RBM或RBM的层次结构提取的特征输入到线性分类器（如线性支持向量机或感知器）中，往往能得到较好的效果。

该模型对输入的分布作了假设。目前，scikit-learn只提供BernoulliRBM，它假设输入是二值(0或1)或介于0和1之间的值，每个值都编码成特定特征被激活的概率。

RBM试图使用特定的图形模型最大化数据的可能性(likelihood)。所使用的参数学习算法（随机最大似然）可防止特征表示偏离输入数据，从而使它们捕获有趣的规律，但使模型对小型数据集的用处不大，且通常对密度估计不起作用。

该方法在具有独立RBMs权值的深层神经网络初始化中得到了广泛的应用。这种方法被称为无监督预训练(unsupervised pre-training)。

示例:

• 用于数字分类的受限玻尔兹曼机器特性

2.9.1.1. 图形模型与参数化

RBM的图形模型是一个全连接的二分图(bipartite graph)。

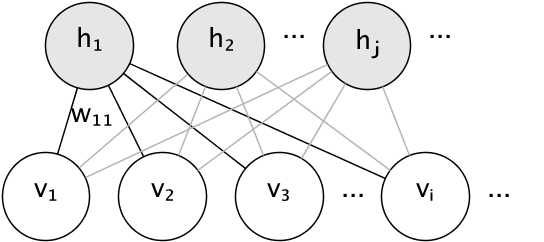
节点是随机变量，其状态取决于它们连接到的其他节点的状态。因此，该模型由连接的权重以及每个可见和隐藏单元的一个偏置(bias)项参数化，为简单起见，将偏置项从上图中省略。

使用能量函数测量联合概率分布的质量：
E(\mathbf{v}, \mathbf{h}) = -\sum_i \sum_j w_{ij}v_ih_j – \sum_i b_iv_i – \sum_j c_jh_j
在上面的公式中，\mathbf{b} 和 \mathbf{c}分别是可见层和隐藏层的偏置向量。模型的联合概率是根据能量定义的：
P(\mathbf{v}, \mathbf{h}) = \frac{e^{-E(\mathbf{v}, \mathbf{h})}}{Z}
受限一词指的是模型的二分结构，它禁止隐藏单元之间或可见单元之间的直接交互。这意味着假设以下条件独立：
h_i \bot h_j | \mathbf{v} \\\ v_i \bot v_j | \mathbf{h}
二分结构允许使用有效的块Gibbs采样(block Gibbs sampling)进行推断。

2.9.1.2. 伯努利限制玻尔兹曼机(Bernoulli Restricted Boltzmann machines)

在 BernoulliRBM中，所有单元都是二元随机单元(binary stochastic units)。这意味着输入数据要么是二值的(0或1)，要么是0到1之间的实数，表示可视单元打开或关闭的概率。这是一个很好的字符识别模型，关注的是哪些像素处于激活状态，哪些像素未激活。对于自然场景的图像，由于背景，深度和相邻像素采用相同值的趋势而不再适合。

每个单元的条件概率分布由其接收的输入的logistic sigmoid激活函数给出：
P(v_i=1|\mathbf{h}) = \sigma(\sum_j w_{ij}h_j + b_i)
P(h_i=1|\mathbf{v}) = \sigma(\sum_i w_{ij}v_i + c_j)

其中，\sigma是logistic sigmoid函数：
\sigma(x) = \frac{1}{1 + e^{-x}}

2.9.1.3. 随机最大似然学习(Stochastic Maximum Likelihood learning)

在BernoulliRBM中实现的训练算法称为随机最大似然（Stochastic Maximum Likelihood learning，简称SML）或持续对比发散（Persistent Contrastive Divergence，简称PCD）。由于数据似然的形式，直接优化最大似然是不可行的：
\log P(v) = \log \sum_h e^{-E(v, h)} – \log \sum_{x, y} e^{-E(x, y)}
为了简单起见，以上公式是针对单个训练示例。相对于权重的梯度由与上述相对应的两个项构成。由于它们各自的符号，它们通常被称为正梯度和负梯度。在这个实现中，梯度是在小批量样本上估计的。

在最大化对数似然的情况下，正梯度使模型更倾向于与观测到的训练数据相容的隐藏状态。由于RBMs的二分结构，可以有效地进行计算。然而，负梯度是难以克服的。它的目标是降低模型所偏好的联合状态的能量，从而使其与数据保持一致。它可以通过马尔可夫链蒙特卡罗(Markov chain Monte Carlo)近似，马尔可夫链蒙特卡罗使用块吉布斯抽样，通过迭代抽样每个给定的v和h，直到链混合。以这种方式生成的样本有时称为幻想粒子(fantasy particles)。这种方法低效且很难确定马尔可夫链是否混合。

对比发散法(Contrastive Divergence method)建议经过少量迭代次数 k (通常是1) 后停止链。该方法速度快，方差小，但样本距离模型分布较远。

持续对比发散(Persistent Contrastive Divergence，即PCD)解决了这个问题。在PCD中，我们不是每次需要梯度时就开始一个新的链，只执行一个Gibbs采样步骤，而是在每次权值更新后保留多个更新了k个Gibbs步骤的链（幻想粒子）。这使得粒子能够更彻底地探索太空。

参考文献:

• “A fast learning algorithm for deep belief nets” G. Hinton, S. Osindero, Y.-W. Teh, 2006
• “Training Restricted Boltzmann Machines using Approximations to the Likelihood Gradient” T. Tieleman, 2008

© 2007 – 2019, scikit-learn 开发人员 (BSD 许可证). 此页显示源码

未经允许不得转载：PythonOK » 2.9. 神经网络模型（无监督）